Calculate the Slope of a Line – Practice Questions
- Posted by Brian Stocker
- Date February 25, 2019
- Comments 3 comments
Finding the Slope of a Line
The slope of a line is the direction and the steepness of the line. Slope is usually the letter m;
Slope is calculated by finding the ratio of the “vertical change” to the “horizontal change” between two points on a line. Sometimes the ratio is expressed as a quotient (“rise over run”), giving the same number for every two points on the line. A line that is decreasing has a negative “rise” and a negative slope.
- If a line is horizontal the slope is zero.
- A line is decreasing if it goes down from left to right. The slope is negative, i.e.
.
- A line is increasing if it goes up from left to right. The slope is positive, i.e.
.
- If a line is vertical the slope is undefined
The rise of a line, between two points, is the difference between the height at those two points, y1 and y2, so the equation is (y2 − y1) = Δy. In basic geometry, we examine short distances, otherwise we would have to incorporate the curvature of the earth. The run, is the difference in distance from a fixed point along a horizontal line, or (x2 − x1) = Δx.
The equation to calculate the slope of a line, m, is:
Calculate the Slopr of a Line - Practice Questions
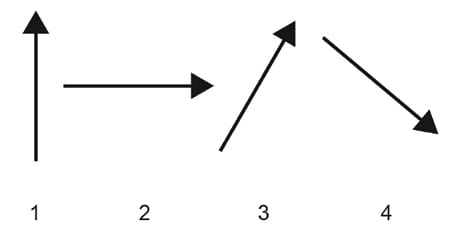
1. What is the correct order of respective slopes for the lines above?
a. Positive, undefined, negative, positive
b. Negative, zero, undefined, positive
c. Undefined, zero, positive, negative
d. Zero, positive undefined, negative
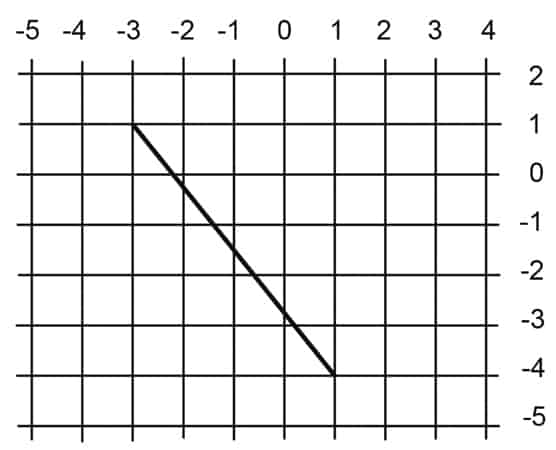
2. Find the slope of the line above.
a. 5/4
b. -4/5
c. -5/4
d. -4/5
3. What is the slope of the line above?
a. 1
b. 2
c. 3
d. -2
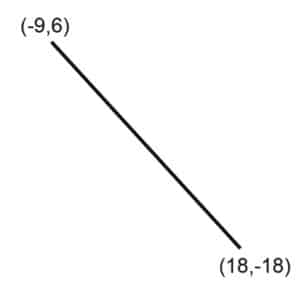
4. What is the slope of the line above?
a. -8/9
b. 9/8
c. -9/8
d. 8/9
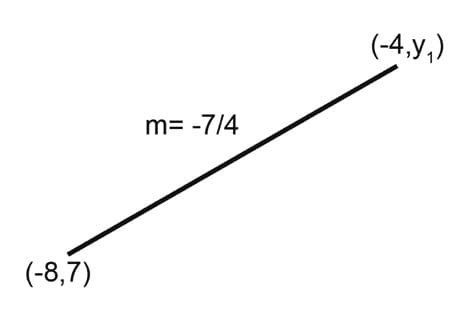
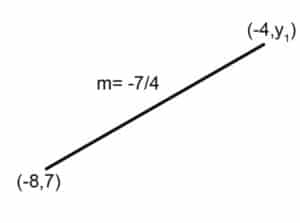
5. With the data given above, what is the value of y1?
a. 0
b. -7
c. 7
d. 8
Answer Key
4. A
(x1, y1) = (-9, 6) & (x2, y2) = (18, -18)
Slope=(-18 – 6) / [18 – (-9)] = -24/27= -(8/9)
Most Popular Geometry Questions
Common geometry questions on on standardized tests :
- Solve for the missing angle or side
- Finding the area or perimeter of different shapes (e.g. triangles, rectangles, circles)
- Problems using the Pythagorean Theorem
- Calculate properties of geometric shapes such as angles, right angles or parallel sides
- Calculating volume or surface area of complex shapes for example spheres, cylinders or cones
- Solve geometric transformations such as rotation, translation or reflections
Most Common Geometry Mistakes on a Test
- Not clearly labeling or identifying the given and unknown information in a problem
- Not understanding the properties and definitions of basic geometric figures (e.g. line, angle, triangle, etc.)
- Incorrectly using basic formulas (e.g. area of a triangle, Pythagorean theorem)
- Incorrectly interpreting geometric diagrams
- Not understanding the relationship between parallel lines and transversals
- Not understanding the relationship between angles and their degree measures
- Not understanding the relationship between perimeter and area
Date Published: Monday, February 25th, 2019
Date Modified: Friday, January 13th, 2023
Got a Question? Email me anytime - Brian@test-preparation.ca
You may also like

Basic Math Video Tutorials

How to Answer Basic Math Multiple Choice




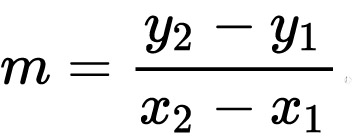



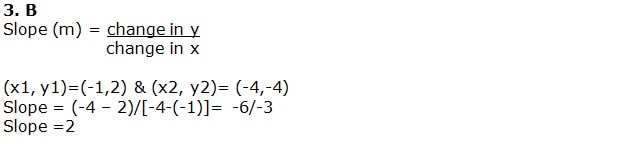
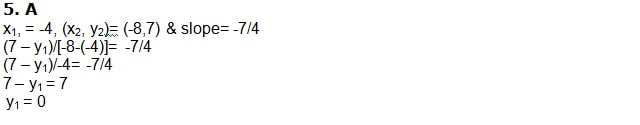
3 Comments
This question is not clear to me.
Which one?
hate geometry 🙁