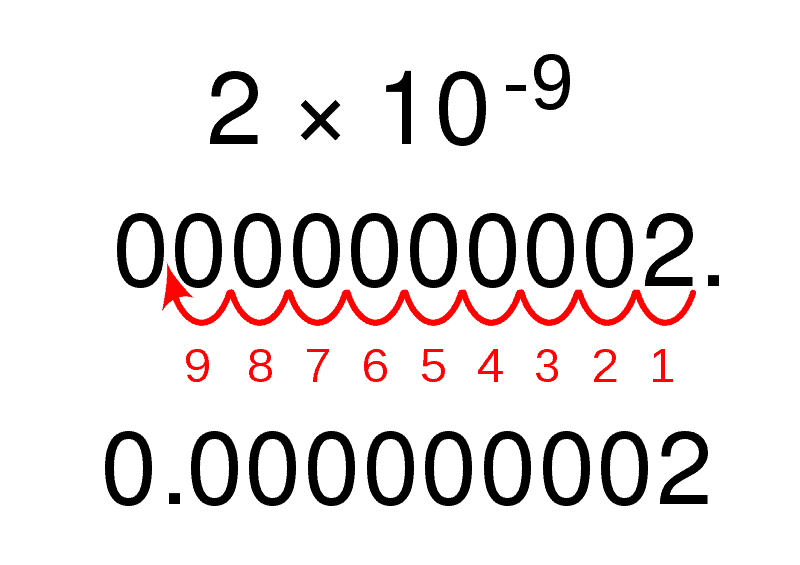
Scientific Notation Math – Tutorial, Examples and Practice Questions

Scientific notation is a way of writing numbers that are too big or too small to be conveniently written in decimal form.

Most High School and exams have scientific Notation questions

To convert a number to scientific notation, place a decimal after the first number that is not a zero, or, after the first number that between 1 and 9.

After placing the decimal, count the number of places the decimal had to move to get the exponent of 10. If the decimal moves to the left, then the exponent to multiply 10 will be in the positive. If the decimal moves from right to left, it will be a negative power of 10.

For example, to convert 29010, we need to place a decimal
after 2, since 2 is the first non zero number. We
would then have 2.90

If we were to convert 0.0167, we need to place the decimal after 1, since the first two numbers before 1 are zeros, and do not fall between 1 and 9. We would thus have 1.67

To complete the conversion of 29010 to scientific notation,
we would get 2.91 x 10⁴

The 10 is raised to the power of 4, because there are 4 places counting from right to left. This scientific notation is positive because the decimal moved to the left.

0.0167 = 1.67 x 10^-2

In this example, the decimal place moved from left to right by 2 spaces thus the 10 is raised to the power of 2. It is negative, because the decimal moved to the right.

You may also need to convert numbers that are already represented in scientific notation or in their power of ten, to regular numbers.
First it is important to remember these two laws.

If the power is positive, shift decimal to the right
If the power is negative, shift decimal point to the left

1. Convert 7,892,000,000 to scientific notation.

A. 7.892 x 10¹⁰
B. 7.892 x 10^-9
C. 7.892 x 10⁹
D. 0.7892 x 10¹¹

2. Convert 0.045 to scientific notation.

A. 4.5 x 10^-2
B. 4.5 x 10²
C. 4.05 x 10-²
D. 4.5 x 10^-3

3. Convert 204 to scientific notation.

A. 2.04 x 10^-2
B. 0.204 x 10²
C. 2.04 x 10³
D. 2.04 x 10²

4.  Convert 0.00002011 to scientific notation.

A. 2.011 x 10^-4
B. 2.011 x 10⁵
C. 2.011 x 10^-6
D. 2.011 x 10^-5

5. Convert this scientific notation back to its original number: 2.63 x 10^-2

A. 0.00263
B. 0.0263
C. 0.263
D. 2.63

6. Convert this scientific notation back to its original number: 5.63 x 10⁶

A. 5,630,000
B. 563,000
C. 5630
D. 0.000005.630

1. C

The decimal point moves 9 spaces right to be placed after 7, which is the first non-zero number. Thus 7.892 x 10⁹

2. A
The decimal point moves 2 spaces to the left to be placed before 4, which is the first non-zero number. Thus its 4.5 x 10^-2 The answer is in negative since the decimal moved left.

3. D
The decimal point moves 2 spaces right to be placed after 2, which is the first non-zero number. Thus it is 2.04 x 10²

4. D
The decimal point moves 5 places left to be placed after 2, which is the first non-zero number. Thus its 2.011 x 10^-5 The answer is in the negative because the decimal moved left.

5. B
The scientific notation is in the negative so we shift the decimal 2 places to the left. Thus its 0.0263.

6. A
The scientific notation is in the positive so we shift the decimal 6 places to the right. Thus it is 5,630,000.

Not using the correct number of significant figures.
This is the most common mistake!   Keep track of the correct number of significant figures.

Forgetting to use a multiplication symbol when converting from standard notation to scientific notation.
Always use a multiplication symbol (e.g., 3 x 10^2 instead of 3 10^2) when working with scientific notation so that you keep everything clear.

Wrong placement of decimal points
Also very common mistake on a test.  Place the decimal point so there is only one non-zero digit to the left of it.

Writing an incorrect exponent form
The exponent to be a power of 10, written as 10^n.

Errors in rounding

Format errors
Always use a consistent format for the exponent, and especially use the correct number of significant figures.

Don’t confuse scientific notation with standard notation
Scientific notation is always to the power of 10.