
How to Solve Linear Equations in one variable – Tutorial and Practice Questions
- Posted by Brian Stocker MA
- Date November 27, 2014
- Comments 3 comments
Quick Review and Tutorial – How to Solve Linear Equations in One Variable
Linear equations in one variable x is an equation with the following form:
ax = b
where a and b are some real numbers. If a = 0 and b is different from 0, then the equation has no solution.
Let’s solve one simple example of a linear equation with one variable:
4x – 2 = 2x + 6
When we are given this type of equations, we are always moving variables to the one side of the equation, and real numbers to the other side of the equals sign. Always remember: if you are changing sides, you are changing signs. Let’s move all variables to the left, and real number to the right side:
4x – 2 = 2x + 6
4x – 2x = 6 + 2
2x = 8
x = 8/2
x = 4
When 2x goes to the left it becomes now -2x, and -2 goes to the right and becomes +2. After calculations, we find that x is 4, which is a solution of our linear equation.
Let’s solve a little more complex linear equation:
(2x – 6)/4 + 4 = x
2x – 6 + 16 = 4x
2x – 4x = -16 + 6
-2x = -10
x = -10/-2
x = 5
We multiply whole equation by 4, to lose the fractional line. Now we have a simple linear equation. If we change sides, we change the signs. At the end we do the final calculations.
Linear Equation in One Variable Practice Questions
1. Solve the linear equation:
-x – 7 = -3x – 9
a. -1
b. 0
c. 1
d. 2
2. Solve the linear equation:
3(x + 2) – 2(1 – x) = 4x + 5
a. -1
b. 0
c. 1
d. 2
3. Find the solution for the following linear equation:
5x/2 = (3x + 24)/6
a. -1
b. 0
c. 1
d. 2
4. If a and b are real numbers, solve the following equation:
(a+2)x-b = -2+(a+b)x
a. -1
b. 0
c. 1
d. 2
5. Find the solution for the following linear equation:
1/(4x – 2) = 5/6
a. 0.2
b. 0.4
c. 0.6
d. 0.8
Answer Key
1. A -1
-x – 7 = -3x – 9
-x + 3x = -9 + 7
2x = -2
x = (-2):2
x = -1
2. C 1
3(x + 2) – 2(1 – x) = 4x + 5
3x + 6 – 2 + 2x = 4x + 5
5x + 4 = 4x + 5
5x – 4x = 5 – 4
x = 1
3. D 2
4. A -1
(a + 2)x – b = -2 + (a + b)x
ax + 2x – b = -2 + ax + bx
ax + 2x – ax – bx = -2 + b
2x – bx = -2 + b
(2 – b)x = -(2 – b)
x=-(2-b):(2-b)
x = -1
5. D 0.8
1/(4x – 2) = 5/6 … We can cross multiply:
5(4x – 2) = 1 * 6 … Now, we distribute 5 to the parenthesis:
20x – 10 = 6 … We need x term alone on one side:
20x = 6 + 10
20x = 16 … Dividing both sides by 20:
x = 16/20 … Simplifying by 2 and having 10 in the denominator provides us finding the
decimal equivalent of x:
x = 8/10 = 0.8
Date Published: Thursday, November 27th, 2014
Date Modified: Monday, June 26th, 2023
You may also like

Basic Math Video Tutorials

How to Answer Basic Math Multiple Choice


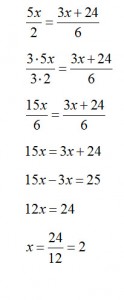
3 Comments
thanks!! found this easy to answer
thanks alot for this preparation
Wow good work